«Мудрость толпы» и ее учет
Чем длиннее игра, тем больше количество наблюдателей появляется в построенных нами зависимых цепях. Каждый наблюдатель может считать себя независимым (его отдельно взятая последовательность абсолютно случайна), и у каждого свои ожидания. Мы видим всех и с каждым новым ходом можем решать, на основании чьих ожиданий делать прогноз в реальной игре, в той последовательности, которая определяется шариком рулетки. Наблюдателей ведь – «толпа», как учесть мнение каждого?
Здесь полезно привести отрывок из книги Джеймса Шуровьески «Мудрость толпы».
В один из осенних дней 1906 года британский ученый Фрэнсис Гальтон оставил свой дом в городе Плимуте и отправился на сельскую ярмарку. Гальтону было восемьдесят пять лет. Он вполне ощущал свой возраст, однако его все еще переполняла любознательность, благодаря которой было написано немало научных трудов по статистике и теориям наследования, принесших ему известность... Гальтон ехал на ежегодную выставку животноводства и птицеводства Западной Англии — региональное мероприятие, на которое собирались местные фермеры и горожане, чтобы оценить достоинства домашнего скота и птицы — коров, овец, лошадей, свиней, кур. Пристало ли именитому ученому (да еще и в столь почтенном возрасте) расхаживать по рядам между загонами и рассматривать рабочих лошадей и свиней-рекордсменок?
Да, в выборе этого странного занятия Гальтон руководствовался логикой. Будучи человеком, буквально одержимым двумя научными увлечениями — оценкой физических и умственных способностей и селекцией, — Гальтон рассматривал животноводческую выставку в качестве огромного стенда, на котором ясно видны результаты удачной и неудачной селекции. Гальтон уделял так много внимания селекции, поскольку полагал, что лишь очень немногие люди обладают данными, необходимыми для поддержания здоровья общества. Значительную часть своей научной карьеры Гальтон посвятил изучению этих данных, как раз чтобы доказать, что подавляющее большинство людей ими не владеет. Например, на Международной выставке 1884 года в Лондоне он устроил "антропометрическую лабораторию", где с помощью приспособлений собственного изобретения проверял посетителей выставки по таким параметрам, как "острота зрения и слуха, способность к различению цвета, избирательность взгляда и время реакции". В результате экспериментов его разочарование в умственных способностях среднестатистического человека усилилось, ибо "тупость и невежество многих мужчин и женщин были настолько велики, что в это трудно было поверить". "Только если власть и управление обществом останутся в руках немногих избранных, безупречных во всех отношениях людей, — сделал вывод Гальтон, — у нас есть будущее".

Вернемся к животноводческой ярмарке. Прогуливаясь по выставке, Гальтон наткнулся на стенд, около которого проводились соревнования по угадыванию веса. На всеобщее обозрение был выставлен откормленный бык, и собравшаяся толпа должна была на глазок определить вес животного. (А точнее, они должны были угадать вес этого быка после того, как его "забьют и освежуют".) За шесть пенсов вы могли купить проштампованный и пронумерованный билет, в который надо было внести ваше имя, адрес и прогноз. За самые точные ответы были обещаны призы.
Счастье попытали примерно восемьсот человек. Это была разношерстная публика — как мясники и фермеры, явно искушенные в оценке веса скота, так и люди, наверняка далекие от животноводства. "Участие приняли множество непрофессионалов, — писал впоследствии Гальтон в научном журнале Nature, — клерки и прочие из тех, кто, не имея специальных знаний о лошадях, делают ставки на бегах, опираясь на мнение газет, друзей или собственное разумение". Гальтону тут же пришла на ум аналогия с демократией, когда люди с радикально различающимися способностями и интересами получают каждый по одному голосу. "Средний участник конкурса был экипирован знаниями для точной оценки веса забитого и освежеванного быка не лучше, чем средний избиратель — для оценки качеств того или иного претендента или особенностей большинства политических вопросов, по которым он голосует", — сетовал он. Гальтон хотел установить, на что способен "средний избиратель", поскольку намеревался доказать, что его возможности очень малы. Поэтому он превратил конкурс в импровизированный эксперимент.
Когда соревнование закончилось и призы были розданы, Гальтон позаимствовал у его организаторов билеты и подверг их ряду статистических тестов. Он рассортировал билеты с прогнозами (всего 787 — ему пришлось исключить тринадцать билетов, ибо они были заполнены неразборчиво) в порядке убывания точности, и выстроил график, чтобы убедиться, что он будет представлять собой колоколообразную, гауссову кривую. Затем он сложил все оценки участников и вывел усредненный прогноз группы. Эта цифра представляла собой, можно сказать, коллективную мудрость плимутской толпы. Если бы толпа была одним человеком, именно так этот человек оценил бы вес быка.
Гальтон, несомненно, полагал, что средний прогноз группы будет очень далек от истины. Казалось очевидным, что коллективное решение толпы, состоящей как из мудрецов, так и из людей посредственных и недалеких, скорее всего окажется неудачным. Но он ошибся.
Толпа предположила, что вес быка, после того как его забьют и освежуют, составит 1197 фунтов. После того как его действительно забили и освежевали, оказалось, что бык весил 1198 фунтов. Иными словами, оценка толпы оказалась очень точной.
Попробуем применить этот подход. Задача каждого нашего наблюдателя – угадать следующее событие в своей цепи. 1 или -1 (читай – красное или черное, чет или нечет, большее или меньшее)?
Так как наблюдатели ожидают реализации всех допустимых возможностей, лучшим предположением о точке зрения отдельно взятого наблюдателя будет, что он ожидает события противоположного случившемуся. Если выпала единица, наблюдатель ожидает «минус один», если минус единица – единицу.
При этом предположении идеально удовлетворяющая ожиданиям последовательность выглядит так: 1-11-11-11-11-11-11-11-11-11... Мы прекрасно видим, она не похожа на случайную. Но вынуждены поверить, как и Фрэнсис Гальтон, что «тупость и невежество (наших наблюдателей) настолько велики», что они не в состоянии это понять. В противном случае придется строить гипотезы о способности наблюдателей распознавать неочевидные закономерности.
Посмотрите, что происходит, когда первый наблюдатель видит «идеальную» картину.
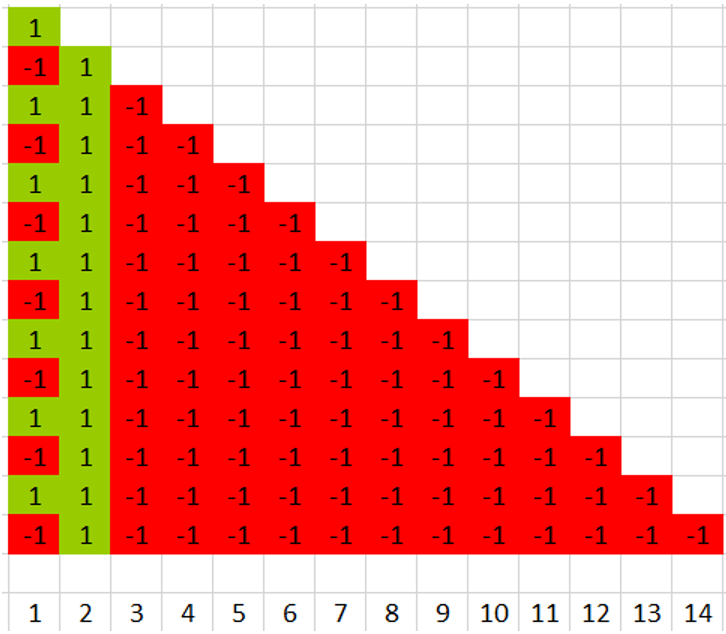
У следующих за ним наблюдателей перед глазами нарастает цепь однородных результатов.
При этом первый наблюдатель на очередном ходе ожидает события -1, и второй наблюдатель тоже ожидает в своей цепи события -1, но, чтобы у второго появился -1, в первой цепи должна выпасть единица. Так как события во всех зависимых цепях определяются результатом исходной, получается, что ожидания первого и второго наблюдателей противоположны, они ждут от Фортуны взаимоисключающих друг друга событий.
Мы также знаем, что «сила» ожидания зависит от количества выпавших подряд одноименных событий. В нашем случае ожидание второго наблюдателя значительно «сильнее», чем первого – тринадцать одноименных результатов против одного. Также заметим, что ожидания наблюдателей 3-14 поддерживают ожидание второго и противоречат ожиданию первого. Баланс явно в пользу того, что в исходной цепи «идеальное» распределение возможных результатов должно как-то закончиться, и после крайней -1 ожидается не «справедливая» 1, а вторая -1.
На что ставим?..
Пред. | След.